1. 마르코프 체인

• 현재 시점에서 특정 상태가 될 확률은 이전 시점 상태에만 영향을 받는 확률 과정을 말한다.

  \[P(X_{t}|X_{t-1}, X_{t-2}, X_{t-3}, ... , X_{0}) = P(X_{t}|X_{t-1})\]

• 각 상태끼리 이동할 확률을 행렬로 나타낸 것이 바로 전이행렬(transition matrix)이다.

  \[\begin{bmatrix} P_{00} & \cdots & P_{0n} \\ \vdots & \ddots & \vdots \\ P_{n0} & \cdots & P_{nn} \end{bmatrix}\]

• 다음 두 가지 식이 성립한다.

  \[P_{ij} = P(X_{n+1}=j|X_{n}=i)\] \[∑_{j=0}^{\infty} P_{ij}=1\]

2. 마르코프 체인의 상태 정리

1) 도달가능 & 교통가능 & 집단(Accessible & Communicative & Class)

• 임의의 \(n\)에 대해서 \(P_{ij}^{(n)} \ge 0\)이면, ‘상태 \(j\)는 상태 \(i\)로부터 도달 가능’하다고 한다.
• 이 관계가 역으로도 성립하면, 두 상태는 서로 교통 가능하다.
• 서로 교통 가능한 상태들을 하나의 집단으로 군집화 할 수 있다.

2) 기약(irreducible)

• 집단이 하나인 마르코프 체인을 말한다. 즉, 모든 상태들이 서로 교통가능한 마르코프 체인이 기약 마르코프 체인이다.
• 기약인 유한 상태 마르코프 체인의 모든 상태는 재귀적이다.
• 

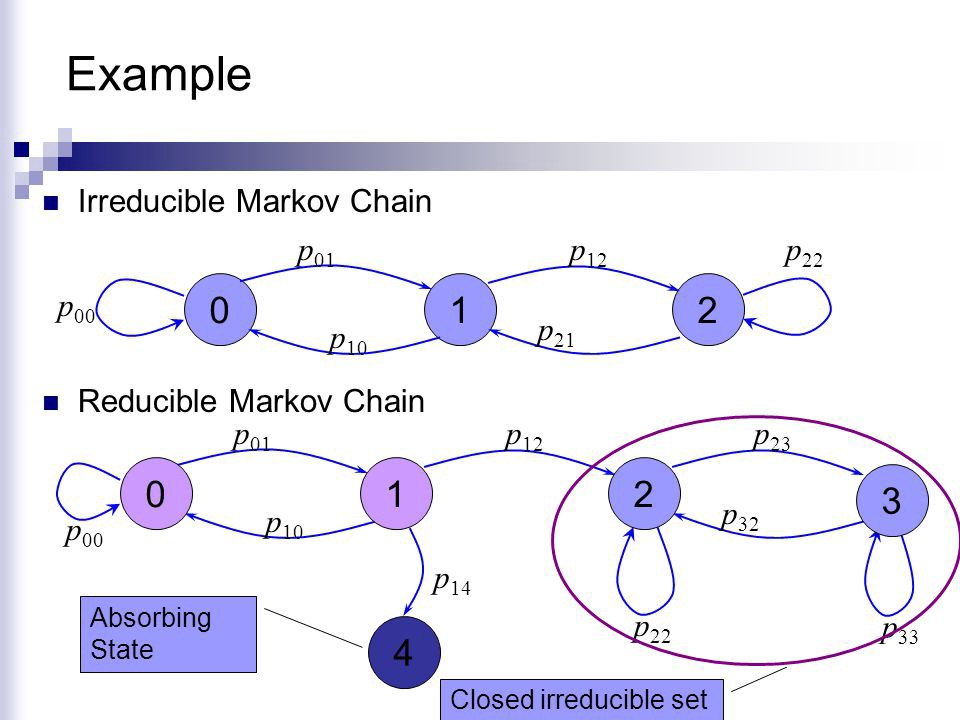
3) 일시(transient) & 재귀(Recurrent)

• 현재 상태를 체인이 전이되면서 다시 돌아오지 못할 수 있다면 일시 상태이다. 즉, 상태 \(i\)로부터 상태 \(j\)는 도달 가능하지만, 상태 \(j\)로부터 상태 \(i\)로 도달할 수 없는 경우이다.
• 반면 반드시 다시 돌아올 수 있다면, 해당 상태는 재귀 상태이다.
• 일시성과 재귀성은 집단 특성이므로, 집단의 특정 상태가 일시적이거나 재귀적이면 다른 모든 상태도 일시적이거나 재귀적이게 된다.

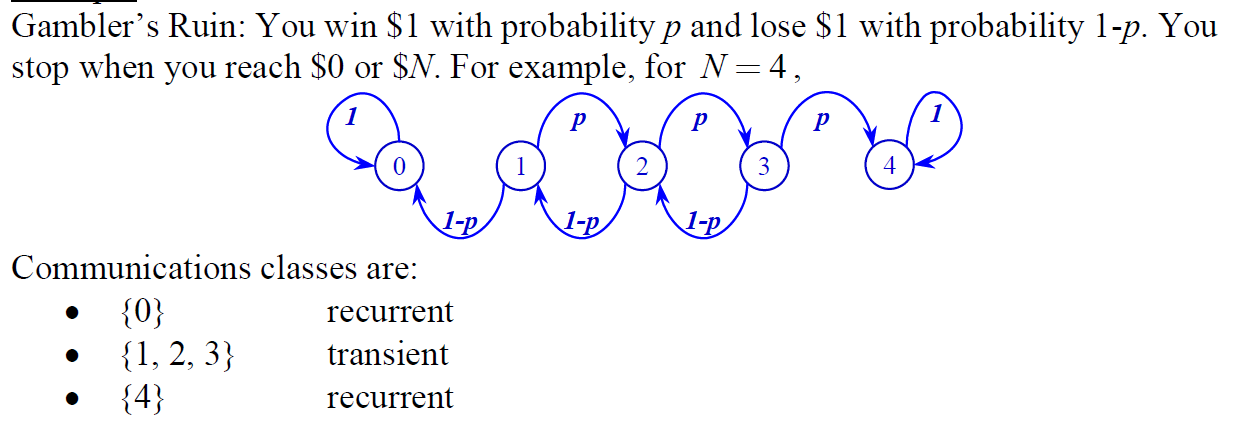
4) 흡수(absorbing)

• 어떤 상태에 들어가면, 자기 자신 외에는 다른 상태로 전이될 수 없는 상태이다.(\(P_{ij} = 1\))
• 흡수 상태는 재귀 상태의 특별한 경우이다.

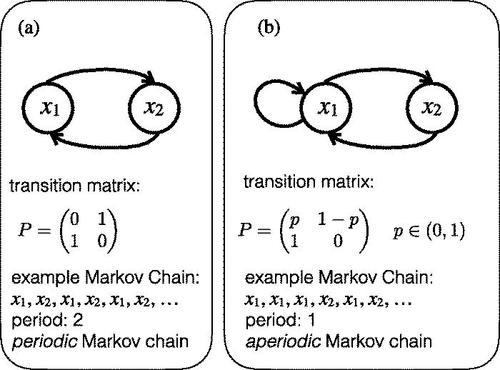
5) 주기(periodic) & 비주기(aperiodic)

• 상태 \(i\)에 대한 주기는 \(n = t, 2t, 3t...\) 이외의 다른 값에 대해서 \(P_{ij}^{(n)} = 0\)을 만족하는 가장 큰 정수 t이다.
• 즉, 상태 \(i\)에서 상태 \(i\)로 돌아오기까지 \(2, 4, 6, ...\)단계가 걸린다면 \(n = 2k - 1 \quad,\quad k = 1,2,3...\)에 대해서 \(P_{ij}^{(n)} = 0\)이므로 주기는 \(2\)이다.
• 반면, 주기 \(1\)을 갖게 되면 비주기 상태이다. 즉, 어떤 과정이 \(s\)와 \(s + 1\) 단계에서 상태 \(i\)에 있을 수 있는 연속된 수 \(s, s + 1\)이 존재하는 경우를 말한다.
• 주기성도 집단 특성이다. 상태 \(i\)가 주기 \(t\)를 가지면, 해당 집단의 모든 상태는 주기 \(t\)를 갖는다.

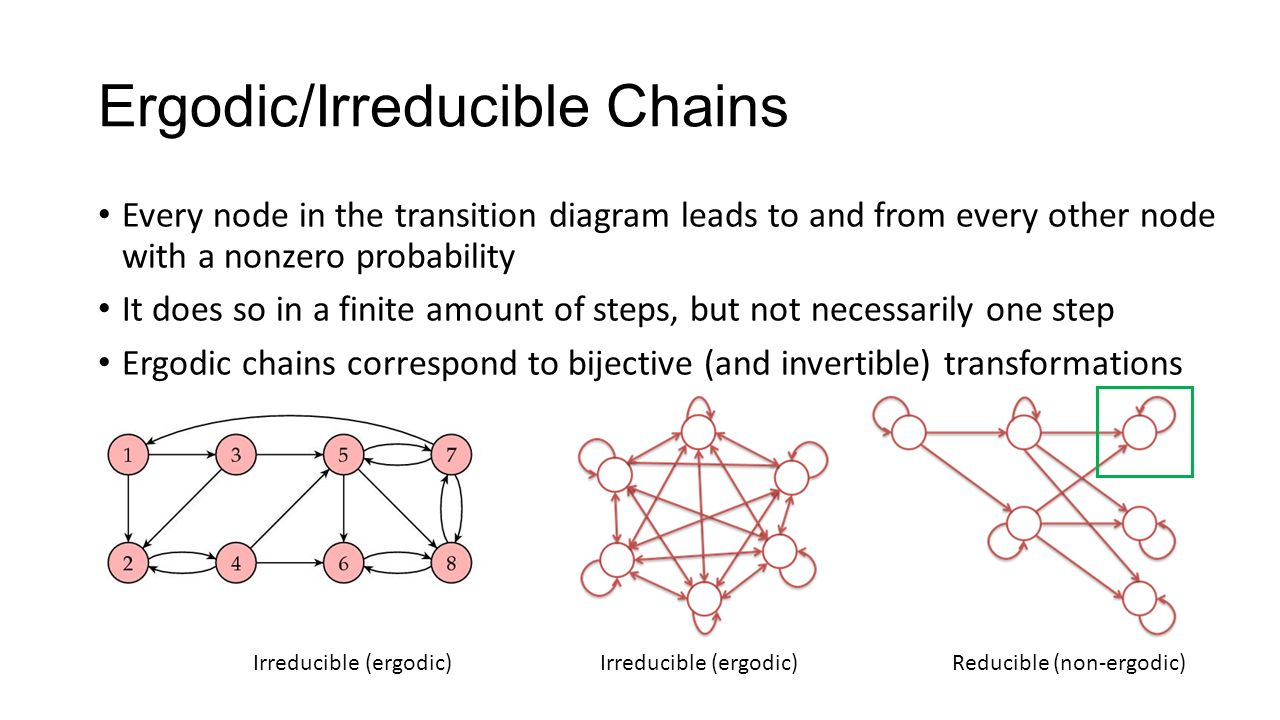
6) 에르고딕(ergodic)

• 유한 상태 마르코프 체인에서 비주기적인(aperiodic) 재귀상태(recurrent)를 말한다.
• 모든 상태가 에르고딕하면 비주기적이고 서로 교통 가능하므로 전체 체인은 irreducible and aperiodic한 마르코프 체인이 되며, 이를 에르고딕 마르코프 체인(Ergodic Markov Chain)이라 한다.
• 이 때, \(n\)단계 전이 확률은 특정한 안정-상태 확률(steady-state probability)로 수렴하게 된다.

3. Stationary Distribution

• 다음 관계식을 만족하는 분포 \(\pi\)를 의미한다.

\[\pi(y) = ∫p(y|x)\pi(x)dx\]

• 즉, \(x\)가 stationary distribution에서 뽑히기 시작했으면, 다음 샘플인 \(y\)도 stationary distribution에서 뽑히게 된다.
• stationary distribution은 없을 수도 있고, 하나가 아닐 수도 있다.
• 여기서 다음 함수를 transition kernel이라고 부른다.

\[p(y|x)\]

4. Detailed Balance Condition

• Transition Kernel \(p\)와 pdf \(π\)가 다음 관계가 있으면 Detailed Balance Condition을 만족한다고 한다.

\[p(y|x)\pi(x) = p(x|y)\pi(y)\]

• Detailed Balance Condition을 만족하면, 분포 \(π\)가 \(X_{t}\)의 Stationary Distribution이 된다.

5. Ergodic Markov Chain

• Ergodic 마르코프 체인은 다음 식을 만족하는 마르코프 체인이다.

\[plim_{n \to ∞} \frac{1}{n} \sum_{t=1}^N h(X_{t}) = ∫h(x)\pi(x)dx\]

• irreducible and aperiodic하면 ergodic 마르코프 체인이 된다.
• 따라서, Posterior Distribution이 Detailed Balance Condition을 만족하는 Ergodic Markov Chain을 만들고, 해당 chain이 수렴한 다음에 샘플을 생성해서 평균을 취하면, 사후 분포 적분을 계산할 수 있다.