1. 상태 정의
state_space = ("sunny", "cloudy", "rainy")
state_info = dict(zip(state_space, np.arange(len(state_space))))
transition_matrix = np.array(((0.6, 0.3, 0.1),
(0.3, 0.4, 0.3),
(0.2, 0.3, 0.5)))
sample_size = 10000
2. 마르코프 체인 생성
def generate_markov_chain(state_info, transition_matrix, sample_size=10000):
initial_state = list(state_info.values())[random.randint(0, len(state_info))]
states = [initial_state]
for i in range(sample_size):
states.append(np.random.choice(tuple(state_info.values()), p=transition_matrix[states[-1]]))
return np.array(states)
3. 수렴성 확인
def plot_markov_chain_convergence(state_space, states, sample_size):
fig, ax = plt.subplots()
width = 1000
offsets = range(1, sample_size, 5)
for i, label in enumerate(state_space): #offset 시점까지 각 상태에 도달했을 확률을 의미.
ax.plot(offsets, [np.sum(states[:offset] == i) / offset for offset in offsets], label=label)
ax.set_xlabel("number of steps")
ax.set_ylabel("likelihood")
ax.legend(frameon=False)
plt.show()
4. 테스트
states = generate_markov_chain(state_info, transition_matrix, sample_size)
plot_markov_chain_convergence(state_space, states, sample_size)
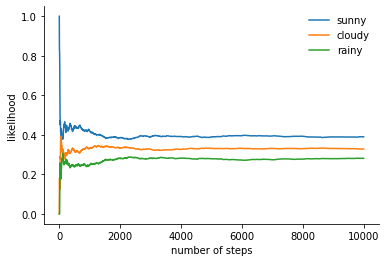
- 전이 횟수가 많아지면서, 확률이 일정한 값으로 수렴하는 것 알 수 있다.