논문 리뷰 (2) - Bayesian Time Series Forecasting with Change Point and Anomaly Detection
06 Aug 2022
Reading time ~6 minutes
개요
논문에서는 이상치 탐지 및 변경점 탐지를 수행하면서 시계열을 예측하는 베이지안 상태 공간 모형을 제안했다. 알고리즘은 초기화, 추론 그리고 예측 세 단계로 구성된다. 논문에서는 알고리즘을 시뮬레이션 된 데이터에 대해서 먼저 적용한 결과를 보여주고 실 데이터에 적용한 결과를 보여준다. 단, 관련된 코드가 공개되어 있지 않아서 이해한 부분까지 구현한 코드를 게시한다. 현재 시뮬레이션 단계에서 이상치 및 변경점을 탐지한 부분까지 구현했다.
실행 결과
현재 단계까지 실행하면, 다음 결과가 나오게 된다. 이상치는 빨간 점, 트렌드 변경점은 주황색 점선으로 표시했다.
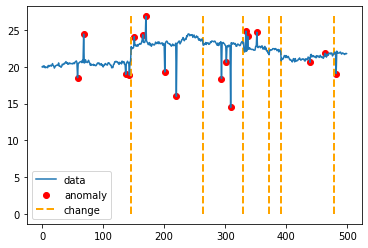
전체 코드
라이브러리 임포트
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
import math
import pykalman
import tensorflow as tf
from scipy import stats
import copy
%matplotlib inline
np.random.seed(1234)
함수화
def init_param():
initial_hidden_variable = [20, 0, 0.1, 0.2, 0.4, -0.1, -0.3, -0.2] #mu, delta, seasonality
sigma_dict = {'e' : 0.1, 'o' : 4, 'u' : 0.1, 'r' : 1, 'v' : 0.0004, 'w' : 0.01} #variance term
anomaly_probability = 10/350
change_probability = 4/350
series_length = 500
return initial_hidden_variable, sigma_dict, anomaly_probability, change_probability, series_length
def indicate_prior_anomaly_change_point(series_length, anomaly_probability, change_probability):
za = np.random.binomial(size=series_length, n=1, p=anomaly_probability) #anomaly indicator
zc = np.random.binomial(size=series_length, n=1, p=change_probability) #change point indicator
zc[330] = 1 #For test
return za, zc
def generate_variances(series_length, sigma_dict):
var_e = np.random.normal(loc=0, scale=sigma_dict['e'],size=series_length)
var_o = np.random.normal(loc=0, scale=sigma_dict['o'],size=series_length)
var_u = np.random.normal(loc=0, scale=sigma_dict['u'],size=series_length)
var_r = np.random.normal(loc=0, scale=sigma_dict['r'],size=series_length)
var_v = np.random.normal(loc=0, scale=sigma_dict['v'],size=series_length)
var_w = np.random.normal(loc=0, scale=sigma_dict['w'],size=series_length)
var_dict = {'e' : var_e, 'o' : var_o, 'u' : var_u, 'r' : var_r, 'v' : var_v, 'w' : var_w}
return var_dict
def indicate_posterior_anomaly_points(anomaly_probability, sigma_dict, za, var_dict, y, mu):
# initialize
posterior_za_probability = []
posterior_za = []
for t in range(len(y)):
if za[t] == 0: #not anomaly point
residual_square = var_dict['e'][t] ** 2
else: #anomaly point
residual_square = var_dict['o'][t] ** 2
# calculate posterior of each casea
anomaly_posterior = (anomaly_probability / sigma_dict['o']) * math.exp(-(residual_square / (2 * (sigma_dict['o'] ** 2))))
normal_posterior = ((1 - anomaly_probability) / sigma_dict['e']) * math.exp(-(residual_square / (2 * (sigma_dict['e'] ** 2))))
# weight average
posterior_anomaly_prob = round(anomaly_posterior / (normal_posterior + anomaly_posterior), 3)
posterior_za_probability.append(posterior_anomaly_prob)
posterior_za.append(np.random.binomial(n=1,p=posterior_anomaly_prob,size=1)[0])
return pd.Series(posterior_za)
def indicate_posterior_change_points(change_probability, sigma_dict, zc, var_dict, y, mu, delta):
# initialize
posterior_zc_probability = []
posterior_zc = []
for t in range(len(y)):
if zc[t] == 0: #not change point
residual_square = var_dict['u'][t] ** 2
else: # change point
residual_square = var_dict['r'][t] ** 2
# calculate posterior of each case
change_posterior = (change_probability / sigma_dict['r']) * math.exp(-(residual_square / (2 * (sigma_dict['r'] ** 2))))
normal_posterior = ((1 - change_probability) / sigma_dict['u']) * math.exp(-(residual_square / (2 * (sigma_dict['u'] ** 2))))
# weight average
posterior_change_prob = round(change_posterior / (normal_posterior + change_posterior), 3)
posterior_zc_probability.append(posterior_change_prob)
posterior_zc.append(np.random.binomial(n=1,p=posterior_change_prob,size=1)[0])
# segment control
posterior_zc = pd.Series(posterior_zc)
posterior_zc = change_point_segment_control(posterior_zc, mu, sigma_dict)
return posterior_zc
def change_point_segment_control(posterior_zc, mu, sigma_dict, segment_length=7):
# find change point index
change_point_index = list(posterior_zc[posterior_zc == 1].index.values)
for index in range(len(change_point_index))[1:]:
# length between two change point is further than segment_length
if change_point_index[index] - change_point_index[index - 1] >= segment_length:
continue
else: # length between two change point isn't further than segment_length
# check differences between one-step before value and one-step ahead value
if np.abs(mu[change_point_index[index - 1] - 1] - mu[change_point_index[index] + 1]) <= sigma_dict['r']/2:
posterior_zc[change_point_index[index - 1]] = 0
posterior_zc[change_point_index[index]] = 0
else:
random_index = np.random.binomial(n=1, p=0.5, size=1)[0]
if random_index == 1:
posterior_zc[change_point_index[index - 1]] = 0
else:
posterior_zc[change_point_index[index]] = 0
return posterior_zc
def generate_time_series(initial_hidden_variable, series_length, za, zc, var_dict, anomaly_probability, change_probability, sigma_dict):
mu = [initial_hidden_variable[0]]
delta = [initial_hidden_variable[1]]
data = [mu[0] + delta[0]]
mu_t = initial_hidden_variable[0]
delta_t = initial_hidden_variable[1]
seasonality = initial_hidden_variable[2:]
y_t = 0
seasonalities = [seasonality]
hidden_state = [[mu_t, delta_t] + seasonality]
for t in range(series_length-1):
# evaluate mu and delta at t using transition equation
if zc[t] == 0:
mu_t = mu_t + delta_t + var_dict['u'][t]
else:
mu_t = mu_t + delta_t + var_dict['r'][t]
delta_t = delta_t + var_dict['v'][t]
# evaluate seasonality at t using transition equation
if t == 330: #For test
seasonality_t = 2
else:
seasonality_t = -sum(seasonality[:t]) + var_dict['w'][t]
# update seasonality array
del seasonality[0]
seasonality.append(seasonality_t)
copied_seasonality = copy.deepcopy(seasonality)
seasonalities.append(copied_seasonality)
# evaluate y at t using observation equation
if za[t] == 0:
y_t = mu_t + delta_t + var_dict['e'][t]
else:
y_t = mu_t + delta_t + var_dict['o'][t]
data.append(y_t)
mu.append(mu_t)
delta.append(delta_t)
hidden_state.append([mu_t, delta_t] + copied_seasonality)
return data, mu, delta, seasonality, seasonalities, hidden_state
def update_standard_deviations(sigma_dict, var_dict, posterior_za, posterior_zc, delta, seasonalities):
not_anomaly = 0
anomaly = 0
for t, anomaly_point in enumerate(posterior_za):
if anomaly_point == 0:
not_anomaly += (var_dict['e'][t] ** 2) / (t + 1)
else:
anomaly += (var_dict['o'][t] ** 2) / (t + 1)
if not_anomaly != 0:
sigma_dict['e'] = math.sqrt(not_anomaly)
if anomaly != 0:
sigma_dict['o'] = math.sqrt(anomaly)
not_chage_point = 0
change_point = 0
for t, change_point in enumerate(posterior_zc):
if change_point == 0:
not_chage_point += (var_dict['u'][t] ** 2) / (t + 1)
else:
change_point += (var_dict['r'][t] ** 2) / (t + 1)
if not_chage_point != 0:
sigma_dict['u'] = math.sqrt(not_chage_point)
if change_point != 0:
sigma_dict['r'] = math.sqrt(change_point)
sigma_dict['v'] = math.sqrt(np.mean(np.square(var_dict['v'])))
gamma = 0
for seasonality in seasonalities:
gamma = math.pow(np.sum(seasonality), 2)
sigma_dict['w'] = math.sqrt(gamma / len(seasonalities))
return sigma_dict
def update_initial_alpha_mean(initial_hidden_variable, generated_smoothed_state_mean):
initial_alpha = initial_hidden_variable[0:2] + list(generated_smoothed_state_mean[6][2:])
return initial_alpha
def test_likelihood_convergence():
return False
def evaluate_likelihood(sigma_dict, var_dict, posterior_za, posterior_zc, delta, seasonalities, anomaly_probability = 10/350, change_probability = 4/350):
log_likelihood = []
for t, anomaly_point in enumerate(posterior_za):
if anomaly_point == 0:
likelihood = stats.norm.logpdf(0, loc=var_dict['e'][t], scale=sigma_dict['e']) # the likelihood g(x1, x2) in the paper is the form of normal density evaluated at 0 with mean x1, standard deviation x2
log_likelihood.append(likelihood)
else:
likelihood = stats.norm.logpdf(0, loc=var_dict['o'][t], scale=sigma_dict['o'])
log_likelihood.append(likelihood)
likelihood = stats.bernoulli.logpmf(k = anomaly_point, p=anomaly_probability)
log_likelihood.append(likelihood)
for t, change_point in enumerate(posterior_zc):
if change_point == 0:
likelihood = stats.norm.logpdf(0, loc=var_dict['u'][t], scale=sigma_dict['u'])
log_likelihood.append(likelihood)
else:
likelihood = stats.norm.logpdf(0, loc=var_dict['r'][t], scale=sigma_dict['r'])
log_likelihood.append(likelihood)
likelihood = stats.bernoulli.logpmf(k = change_point, p=change_probability)
log_likelihood.append(likelihood)
for t, delta_variance in enumerate(var_dict['v']):
likelihood = stats.norm.logpdf(0, loc=delta_variance, scale=sigma_dict['v'])
log_likelihood.append(likelihood)
for t, seasonality in enumerate(seasonalities):
likelihood = stats.norm.logpdf(0, loc=-np.sum(seasonality), scale=sigma_dict['w'])
log_likelihood.append(likelihood)
return np.exp(np.sum(log_likelihood))
알고리즘 실행 단계 정의
def initialization():
initial_hidden_variable, sigma_dict, anomaly_probability, change_probability, series_length = init_param()
za, zc = indicate_prior_anomaly_change_point(series_length, anomaly_probability, change_probability)
var_dict = generate_variances(series_length, sigma_dict)
return initial_hidden_variable, series_length, za, zc, var_dict, anomaly_probability, change_probability, sigma_dict
def inference(initial_hidden_variable, series_length, za, zc, var_dict, anomaly_probability, change_probability, sigma_dict):
is_likelihood_converged = test_likelihood_convergence()
count = 0
while count < 1:
is_likelihood_converged = True # Remove after implementing likelihood function convergence logic
a_one = initial_hidden_variable[0]
# infer alpha by kalman filter, kalman smoother and fake-path trick. Maybe like this?
## 1. generate time series
generated_data, mu, delta, seasonality, seasonalities, hidden_state = generate_time_series(initial_hidden_variable, series_length, za, zc, var_dict, anomaly_probability, change_probability, sigma_dict)
## 2. Calculate $E(\tilde\alpha$ | \tildey)$ by applying kalman filter and kalman smoother to generated time series
kalman_filter_for_generated_data = pykalman.KalmanFilter(initial_state_mean = generated_data[0], n_dim_obs=1)
generated_filtered_state_mean, generated_filtered_state_covariance = kalman_filter_for_generated_data.em(generated_data).filter(generated_data)
generated_smoothed_state_mean, generated_smoothed_state_covariance = kalman_filter_for_generated_data.smooth(generated_filtered_state_mean)
'''
## 3. Calculate $E($\alpha$ | $y$)$ by applying kalman smoother to real time series
kalman_filter_for_real_data = pykalman.KalmanFilter(initial_state_mean = real_data[0], n_dim_obs=1)
real_filtered_state_mean, real_filtered_state_covariance = kalman_filter_for_real_data.em(real_data).filter(real_data)
real_smoothed_state_mean, real_smoothed_state_covariance = kalman_filter_for_real_data.smooth(real_filtered_state_mean)
## 4. sample alpha
fake_path_trick_result = mu - generated_smoothed_state_mean + real_smoothed_state_mean
'''
# update prior anomaly point and change point indicators with segment control
posterior_za = indicate_posterior_anomaly_points(anomaly_probability, sigma_dict, za, var_dict, generated_data, mu)
posterior_zc = indicate_posterior_change_points(change_probability, sigma_dict, zc, var_dict, generated_data, mu, delta)
# calculate log likelihood with sigma update
sigma_dict = update_standard_deviations(sigma_dict, var_dict, posterior_za, posterior_zc, delta, seasonalities)
# update a1
# initial_hidden_variable = update_initial_alpha_mean(initial_hidden_variable, generated_smoothed_state_mean)
# evaluate log_likelihood
likelihood = evaluate_likelihood(sigma_dict, var_dict, posterior_za, posterior_zc, delta, seasonalities)
count += 1
# plot result
zc = posterior_zc[posterior_zc==1]
za = posterior_za[posterior_za==1]
anomaly = pd.Series(generated_data)
anomaly_data = anomaly[za.index + 1]
plt.plot(generated_data, label='data')
plt.plot(generated_filtered_state_mean, label='generated_data_filtered_state', color='green')
plt.plot(generated_smoothed_state_mean, label='generated_data_smoothed_state', color='yellow')
plt.scatter(anomaly_data.index, anomaly_data.values, label='anomaly', color='red')
plt.vlines(x=list(zc.index.values), ymax = [max(generated_data)] * len(zc.index), ymin = [0] * len(zc.index), label='change', colors='orange', ls='--', lw=2)
plt.legend()
def forecasting():
pass
실행
def main():
initial_hidden_variable, series_length, za, zc, var_dict, anomaly_probability, change_probability, sigma_dict = initialization()
inference(initial_hidden_variable, series_length, za, zc, var_dict, anomaly_probability, change_probability, sigma_dict)
forecasting()
main()